不重复造轮子了，直接放链接学习……相关描述为直接转载

模型评估

性能度量

准确率（查准率）

所有 预测为正例 的样本中 真正例的占比，**查准率**，$$Precision=\frac{TP}{TP+FP}$$

召回率（查全率）

所有 实际为正例 的样本中 真正例的占比，**查全率**，$$Recall=\frac{TP}{TP+FN}$$

F-score

基于查全率和查准率的 调和平均，$$\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R}) \Rightarrow F1=\frac{2 \times P \times R}{P+R}$$

真正例率

正样本中预测为正例（预测对的正样本）的占比，$$TPR=\frac{TP}{TP+FN}=Recall$$

假正例率

负样本中预测为正例（预测错的正样本）的占比，$$FPR=\frac{FP}{TN+FP}$$

P-R曲线与ROC曲线的区别

ROC曲线和P-R曲线选择

P-R曲线与ROC曲线的区别与选择
（1）应用场景
ROC曲线：一般用于分类的场景，二分类多分类皆可。比如我们的测试集右正样本和负样本，通过测试就可以得到 TPR 和 FPR。
P-R曲线：一般用于目标检测领域。通过我们前面的介绍，可以看到 precision 表示预测为正例中有多少是真正的正例，即表示出了预测的准不准。在目标检测领域，例如典型的飞机、船检测，都是从图像中检测出上述目标，那么不可避免的就会有背景 (FP) 出现，进而可以计算 precision。一个好的目标检测模型，P-R 曲线下的面积 (AUC) 越大。
（2）正负样本不均衡下的鲁棒性
ROC曲线：正负样本不均衡下更稳定。在实际的数据集中经常会出现类不平衡 (class imbalance) 现象，即负样本比正样本多很多(或者相反)，而且测试数据中的正负样本的分布也可能随着时间变化。例如当负样本增加时，TPR 是不变的，根据下式可知，FP 同在分子和分母，则变化也不大，因此 ROC 的曲线变化不大。
P-R曲线：受到正负样本分布影响较大。仍以上面的例子为例，当负样本增加时，recall 是不变的，根据下式可知，FP 在分母，则 precision 会明显的降低。

总结：
（1）一般的分类任务，采用 ROC 曲线；
（2）当正负样本比例失调时，则 ROC 曲线变化不大，此时用 PR 曲线更加能反映出分类器性能的好坏。

模型检验方法

模型评估时常用的验证方法有哪些？

（1）Holdout
（2）K-Fold
（3）自助法

线性模型

Logistic回归

逻辑回归（Logistic Regression）详解

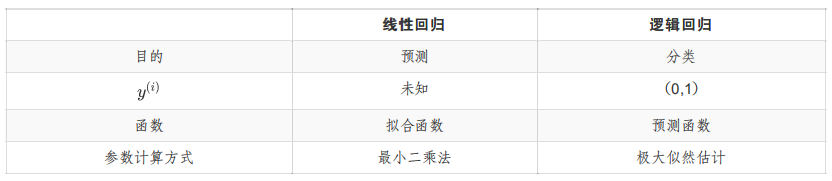
（1）逻辑回归和线性回归的区别？
解析：

（2）逻辑回归为什么选择对数损失函数？
解析：为了优化过程中得到的是全局最优解，一般要求逻辑回归的损失函数为凸函数，而相比于平方损失，对数函数的二阶导恒大于 $0$（可严格 证明）。

线性判别分析（LDA）

Linear Discriminant Analysis, LDA

通俗易懂的描述：采用 “投影后类内方差最小，类间方差最大” 的思想将高维空间的数据 降一维 投影到一条直线上（或超平面）。

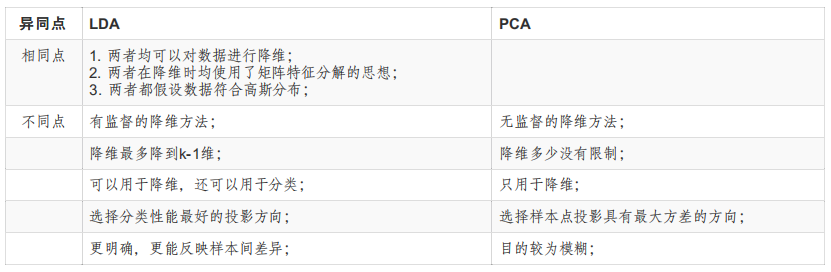
与 PCA 降维的区别

优化方法

凸函数

梯度下降法与牛顿法

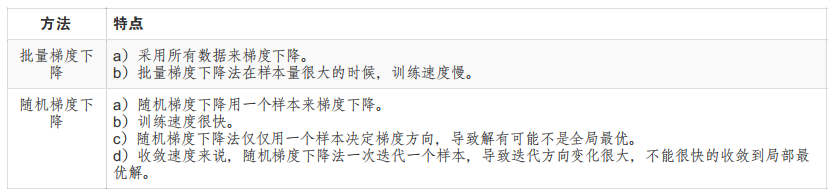
梯度下降的三种方式：批量梯度下降（BGD）、随机梯度下降法（SGD）、小批量梯度下降（MBGD）

梯度下降法和牛顿法的总结与比较

梯度下降法与牛顿法的对比
（1）牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。
优点：收敛速度很快。海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。
缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法（拟牛顿法）。
（2）梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。
越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。

欠拟合（高偏差）和过拟合（高方差）

以下搬运自：入坑机器学习：六，逻辑回归

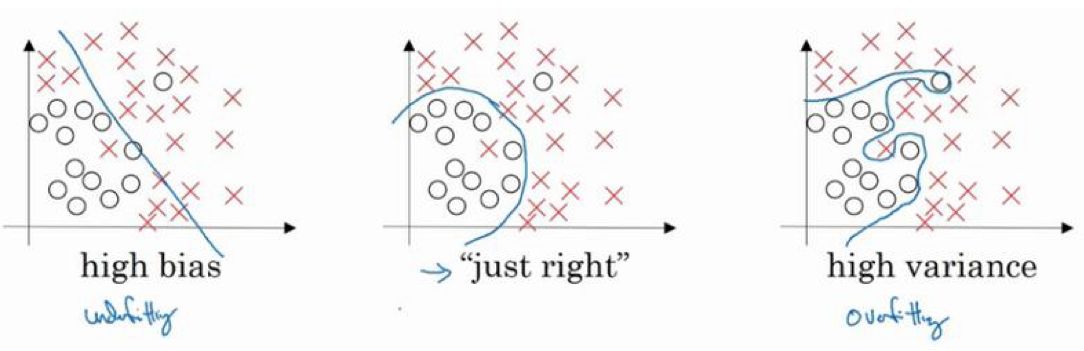
从左至右为：
（1）线性模型，欠拟合，不能很好地适应我们的训练集；
（2）似乎最合适；
（3）四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。可以看出，若给出一个新的值使之预测，它将表现的很差，即过拟合。

如何处理过拟合问题?
（1）特征选择。丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一 些模型选择的算法来帮忙（例如 PCA）；
（2）正则化。保留所有的特征，但是减少参数的大小（Magnitude，指参数的数值大小）。高次项导致了过拟合的产生，使高次项的系数接近于 0 即可。

代价函数

常见的代价函数（以逻辑回归为例）：

均方误差 MSE：$J(\theta)=\frac{1}{2m}[\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}+\lambda\sum_{j=1}^{m}\theta_{j}^{2}]$

交叉熵 CE：$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}[-y^{(i)}log(h_{\theta}(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]+\lambda\sum_{j=1}^{m}\theta_{j}^{2}$

（1）$\lambda$ 称为正则化参数或惩罚系数（同 SVM 中的系数 C），增加 $\lambda\sum_{j=1}^{m}\theta_{j}^{2}$ 一项为什么能减少参数 $\theta$ 的值？
解析：一般情况下，正则化系数 $\lambda$ 的设定值会比较大，$J(\theta)$ 在使得代价最小的过程中只能通过减少 $\theta$ 的值来实现。
（2）为什么代价函数要具有非负性？
解析：保证设计的目标函数有下界，才能确保在优化过程中使其不断减小，直至收敛。

正则化（Regularization）和稀疏性（重点）

什么叫正则化？
正则化，也称规则化，旨在给需要训练的目标函数（作用于模型参数）加上一些规则和限制。

L2正则化、L1正则化与稀疏性

L1正则化及其稀疏性的傻瓜解释

L1 和 L2 的区别
（1）L1 是模型各个参数的绝对值之和；L2 是模型各个参数的平方和的开方值。
（2）L1 会趋向于产生少量的特征，而其他的特征都是 0。因为最优的参数值很大概率出现在坐标轴上，这样就会导致某一维的权重为 0 ，产生稀疏权重矩阵。
（3）L2 会选择更多的特征，这些特征都会接近于 0。最优的参数值很小概率出现在坐标轴上，因此每一维的参数都不会是0。当最小化 $||w||$时，就会使每一项趋近于 0。
（4）L1 的作用是为了矩阵稀疏化。假设的是模型的参数取值满足拉普拉斯分布。
（5）L2 的作用是为了使模型更平滑，得到更好的泛化能力。假设的是参数是满足高斯分布。

Dropout
通过随机删除⽹络中的神经单元，使得模型拟合不依赖于任何⼀个特征；

决策树

ID3，C4.5，CART决策树

贝叶斯分类器

朴素贝叶斯分类器

推导以及假设条件

支持向量机

  • 当训练样本线性可分时，通过硬间隔（hard margin）最⼤化，学习⼀个 线性可分⽀持向量机；
  • 当训练样本近似线性可分时，通过软间隔（soft margin）最⼤化，学习⼀个 线性⽀持向量机；
  • 当训练样本线性不可分时，通过核技巧和软间隔最⼤化，学习⼀个 ⾮线性⽀持向量机；

原问题

样本空间中任意点 $x$ 到超平面 $(w, b)$ 的距离可定义为 $$r=\frac{|w^{T}x+b|}{||w||},$$ 超平面的分类策略为 $$\begin{cases} w^{T}x+b \geq +1, y_{i}=+1; \\ w^{T}x+b \leq -1, y_{i}=-1. \end{cases}$$ 两个异类 支持向量（使得上式取等号的样本点，即$|w^{T}x+b|=1$）到超平面的距离和（即间隔）为 $$margin=\frac{2}{||w||},$$ 优化目标即为 找到一个超平面，使得间隔最大，问题定义为 $$\max_{w,b} \frac{2}{||w||},$$ 等价于 $$\min_{w,b} \frac{1}{2}||w||^{2},$$ $$\text{s.t. } y_{i}(w^{T}x_{i}+b) \ge 1, i=1,2,…,m.$$

对偶问题

SVM 对偶形式的推导，以及 Gurobi 求解对偶形式 SVM

注：优化问题的约束条件一般写成标准形式，即左小右大且右侧为 $0$，因此约束条件转化为 $1-(y_{i}(w^{T}x_{i}+b) \le 0$ 的形式再构造拉格朗日函数。

显然，原问题是一个凸二次规划问题，其拉格朗日函数可以写成：
$$L(w,b,\alpha)=\frac{1}{2}||w||^{2}+\sum_{i=1}^{m}\alpha_{i}(1-(y_{i}(w^{T}x_{i}+b))),$$ 由 $\alpha_{i}(1-(y_{i}(w^{T}x_{i}+b) \le 0$，可知 $L(w,b,\alpha) \le \frac{1}{2}||w||^{2}$，即 拉格朗日函数是原问题的一个下界。

我们要想找到最接近原问题最优值的一个下界，就需要 求出下界的最大值，即 $\max_{\alpha} L(w,b,\alpha)$，则原问题可转化为优化问题： $$\min_{w,b}\max_{\alpha} L(w,b,\alpha),$$ 根据拉格朗日对偶性，原问题（极小极大问题）等价于其对偶问题（极大极小问题）： $$\max_{\alpha}\min_{w,b} L(w,b,\alpha).$$

为什么要将原问题转换成对偶问题？
（1）问题求解。$\min_{w,b}\max_{\alpha} L(w,b,\alpha)$ 形式的极小极大问题只能对 $\alpha$ 求导，转化为极大极小问题 $\max_{\alpha}\min_{w,b} L(w,b,\alpha)$ 后才能对求导以求最优解；
（2）降低复杂度。将求特征向量 $w$（复杂度为 $O(d)$）转化为求比例系数 $\alpha$（复杂度为 $O(m)$），其中 $d$ 为样本的维度，$m$ 为样本数量。 关键在于：只有支持向量的比例系数 $\alpha$ 才非 $0$；
（3）约束转换。将不等式约束转换成等式约束；
（4）方便核函数的引入？

对偶变换成立的条件是什么？
解析：KKT 条件。KKT条件是原问题与对偶问题等价的必要条件，当原问题是凸优化问题时，变为充要条件。

求解的问题明确了，接下来就是简化问题和推导约束条件的过程，将 $L(w,b,\alpha)$ 分别对 $w$ 和 $b$ 求偏导可得 $$\begin{aligned} \frac{\partial L}{\partial w}&=w-\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}, \\ \frac{\partial L}{\partial b}&=-\sum_{i=1}^{m}\alpha_{i}y_{i},\end{aligned}$$ 令上述两式为 $0$，可得 $$w=\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i},$$ $$\sum_{i=1}^{m}\alpha_{i}y_{i}=0,\tag{*}$$ 将 $w=\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}$ 带入拉格朗日函数 $L(w,b,\alpha)$ 中，可得 $$\begin{aligned} L(w,b,\alpha)&=\frac{1}{2}w^{T}w+\sum_{i=1}^{m}\alpha_{i}(1-(y_{i}(w^{T}x_{i}+b))) \\ &=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}+\sum_{i=1}^{m}\alpha_{i}-\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}-b\sum_{i=1}^{m}\alpha_{i}y_{i} \\ &=\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}, \end{aligned}$$ 将上述简化后的问题结合 $(*)$ 式的约束即为最后的对偶问题：
$$\max_{\alpha}\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j},$$ $$\begin{aligned} \text{s.t. } &\sum_{i=1}^{m}\alpha_{i}y_{i}=0, \\ &\alpha_{i} \ge 0, i=1,2,…,m. \end{aligned}$$

KKT条件

KKT 条件是非线性问题有最优解的充分必要条件

等式约束问题可按拉格朗日乘数法直接求解。对于不等式约束问题
$$\min f(x)$$ $$\text{s.t. } g(x) \le 0$$
其最优解必然在可行域内部或边界上，设该问题的拉格朗日函数为 $L(x,\lambda)=f(x)+\lambda g(x)$。
（1）当最优解 $x^{*}$ 落在可行域内部，即 $g(x^{*})<0$，此时约束条件 $g(x) \le 0$ 无效，等效于令 $$\begin{cases} \lambda = 0 \\ \nabla_{x} L(x,\lambda)=\nabla f(x)=\frac{\partial f(x)}{\partial x}=0, \end{cases}$$ 即可求得最优解；
（2）当最优解 $x^{*}$ 落在可行域边界，即 $g(x^{*})=0$，此时可视为等式优化问题，同样利用拉格朗日函数求解，令 $$\nabla_{x} L(x,\lambda)=\nabla f(x^{*})+\lambda \nabla g(x^{*}),$$ 可以证明 $\nabla f(x^{*})$ 与 $\nabla g(x^{*})$ 方向必然相反（数学证明未找到），因此必然存在 $\lambda >0$ 使得 $\nabla f(x^{*})+\lambda \nabla g(x^{*})=0$ 有解，该解即为最优解。
整合以上两种情况，必然存在以下条件：
$$\begin{cases} \nabla_{x} L(x,\lambda)=\nabla f(x)+\lambda \nabla g(x)=0 \\ g(x) \le 0 \\ \lambda \ge 0 \\ \lambda g(x) = 0 \end{cases}$$
以上条件合称 KKT 条件，分别为定常方程式、原始可行性、对偶可行性，以及互补松弛性；

由于 SVM 的 原问题为不等式约束问题，其对偶问题必须满足 KKT 条件，即：
$$\begin{cases} \nabla_{x} L(w,b,\alpha)=0 \\ 1-y_{i}(w^{T}x_{i}+b) \le 0 \\ \alpha_{i} \ge 0 \\ \alpha_{i} (1-y_{i}(w^{T}x_{i}+b)) = 0. \end{cases}$$

核函数

为什么引入核函数？
解析：实际数据往往是线性不可分的，通过引入核函数将特征映射到更高维的空间实现分类。

核函数的引入是否大大增加了计算复杂度？
解析：没有。核函数将特征进行低维到高维的转化，但实际上是在低维的空间上计算得到高维空间的效果，不会出现维度爆炸或计算复杂度急剧上升的问题。

核函数的本质？
解析：核函数是一个低维的计算结果，并没有真正实现低维到高维的映射，而是 核函数低维运算的结果等价于映射到高维时向量点积的值。
假设高维空间中两个向量 $x_{i},x_{j}$ 的内积为 $I=<x_{i},x_{j}>$，映射之后高维空间中的内积为 $I’=<\Phi(x_{i}),\Phi(x_{j})>$，尝试找到一个函数使得 **低维空间的向量 $x_{i},x_{j}$ 的运算结果为 $K(x_{i},x_{j})=I’$**，其中 $K(x,y)$ 即为核函数。

明确了以上三个问题，核函数的引入动机和作用方式也就很清楚了。

常用核函数

名称表达式参数优势-
线性核$\kappa(x_{i},x_{j})=x_{i}^{T}x_{j}$-
多项式核$\kappa(x_{i},x_{j})=(x_{i}^{T}x_{j})^d$$d(\ge 1)$，为多项式的次数较线性核而言，可解决非线性问题
高斯核$\kappa(x_{i},x_{j})=\exp(-\frac{||x_{i}-x_{j}||^{2}}{2\sigma^{2}})$$\sigma(> 0)$，为高斯核的带宽可映射到无限维
指数核$\kappa(x_{i},x_{j})=\exp(-\frac{||x_{i}-x_{j}||}{2\sigma^{2}})$$\sigma(> 0)$调整向量距离为 $L1$ 距离，对参数的依赖性降低
拉普拉斯核$\kappa(x_{i},x_{j})=\exp(-\frac{||x_{i}-x_{j}||}{\sigma})$$\sigma(> 0)$基本等价于指数核，对参数的敏感性更低
Sigmoid核$\kappa(x_{i},x_{j})=\tanh(\beta x_{i}^{T}x_{j}+\theta)$$\tanh$ 为双曲正切函数，$\beta > 0, \theta < 0$-

软间隔和正则化

软间隔：允许某些样本不满足约束 $y_{i}(w^{T}x_{i}+b) \ge 1$。

优化目标的改进

在 最大化间隔的同时，使得不满足约束的样本尽可能少，优化目标写成：$$\min_{w,b} \frac{1}{2}||w||^{2}+C \sum_{i=1}^{m}\mathcal{L}(z),$$ 以上问题可称为正则化问题，其中 $C$ 为惩罚系数，$C$ 越大，上式会迫使更多的样本满足约束，反之更少。

软间隔SVM的欠拟合和过拟合解决办法？
解析：欠拟合-增大 $C$，过拟合-减小 $C$。

SVM的优劣势

SVM的优点：
（1）解决了 小样本情况下 的机器学习分类问题。
（2）由于使用核函数方法 克服了维数灾难和非线性可分的问题，所以向高维空间映射时没有增加计算的复杂度。（由于支持向量机算法的最终决策函数只由少数的支持向量所确定，所以计算的复杂性取决于支持向量的数目，而不是整个样本空间的维数）。

SVM的缺点：
（1）支持向量机算法对大规模训练样本难以实施，这是因为支持向量算法借助二次规划求解支持向量，这其中会设计 $m$ 阶矩阵的计算，所以 矩阵阶数很大时将耗费大量的机器内存和运算时间。
（2）经典的 SVM 只给出二分类的算法，而在数据挖掘中，一般要解决多分类的分类问题，而支持向量机 对于多分类问题解决效果并不理想。
（3）现在常用的 SVM 理论都是使用 **固定惩罚系数 $C$**，但是正负样本的两种错误造成的损失是不一样的。

一些问题

神经网络

感知机

BP神经网络

深度学习

For Offersssss! （深度学习篇）

聚类

原型聚类

K-Means

算法步骤：
假设样本总数为 N，K-means 聚类法可以简单表示为一下几个步骤：
（1）在样本中随机选取 K 个点，作为每一类的中心点。
（2）计算剩下 n-K 个样本点到每个聚类中心的距离（距离有很多种，假设这里采用欧式距离）。对于每一个样本点，将它归到和他距离最近的聚类中心所属的类。
（3）将每一个类内的所有点取平均值，计算出新的聚类中心。
（4）重复步骤 2 和 3 的操作，直到所有的聚类中心不再改变。

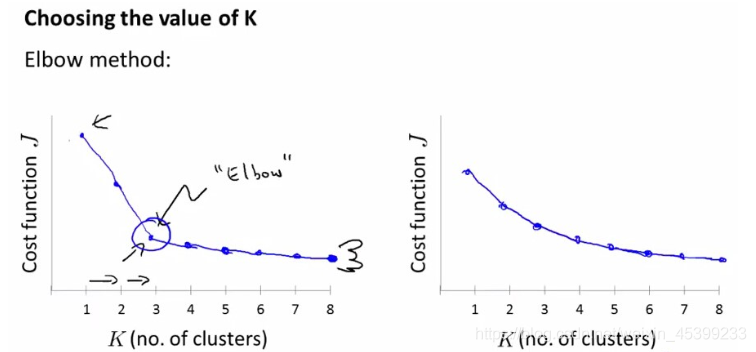
K值的选择？
（1）拍脑袋法：$K \approx \sqrt{n/2}$
（2）肘部法则：纵坐标 cost 一般可以定义为 Sum of the Squared Srrors（SSE），$SSE=\sum_{p \in C_{i}}|p-m_{i}|^{2}$，其中 $C_{i}$ 代表第 $i$ 个簇，$p$ 是簇 $C_{i}$ 里的样本点，$m_{i}$ 是簇的中心。如下左图为一个比较完美的肘部图，但不是所有的问题都能画出这样的图，因此对于 右图无法确认的情况则需要借助其他的方法。

（3）轮廓系数法：定义样本点 $X_{i}$ 的轮廓系数（Silhouette Coefficient）为 $$S_{i}=\frac{b(i)-a(i)}{max(a(i),b(i))}=\begin{cases} 1-\frac{a_{i}}{b_{i}}, a_{i}<b_{i}, \\ 0, a_{i}=b_{i}, \\ \frac{b_{i}}{a_{i}}-1, a_{i}>b_{i}, \end{cases}$$ 易知 $S_{i} \in [-1,1]$，其中 $a_{i}$ 是 $X_{i}$ 和同簇的其他样本的平均距离，称为 簇内差异度。 $b_{i}$ 是 $X_{i}$ 和最近簇中所有样本的平均距离，称为 簇间差异度。 由上式可知：
i）若 $a_{i}<b_{i}$，则 $S_{i} \rightarrow 1$，表示簇内相似度足够高，样本 $X_{i}$ 的聚类结果合理；
**ii）**若 $a_{i}>b_{i}$，则 $S_{i} \rightarrow -1$，表示簇内相似度不足，样本 $X_{i}$ 应该聚类到另外的簇。
iii）若 $a_{i}=b_{i}$，则 $S_{i} \approx 0$，说明样本 $X_{i}$ 在两个簇的边界上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np

class K-Means:

    def __init__(self, k, iter_num):
        self.k = k
        self.iter_num = iter_num

    def fit(self, data):
        data = np.asarray(data)
        np.random.seed(0)

        self.cluster_centers = data[np.random.randint(0, len(data), self.k)]
        self.classes = np.zeroes(len(data))

        for iter in range(iter_num):
            # 计算每个样本 x 距离聚类中心的距离，更新样本类别为最近的聚类中心所属类别
            for index, x in enumerate(data):
                distance = np.sqrt(np.sum((x - self.cluester_center)**2, axis=1))
                self.classes[index] = distance.argmin()

            # 更新 K 个聚类中心
            for i in range(self.k):
                self.cluster_center[i] = np.mean(data[self.classes == i], axis=0)

    def predict(self, data):
        data = np.asarray(data)
        pred = np.zeroes(len(data))

        for index, x in enumerate(data):
            distance = np.sqrt(np.sum((x - self.cluester_center)**2, axis=1))
            pred[index] = distance.argmin()

        return pred

高斯混合模型（GMM）

降维

线性判别分析（LDA）

主成分分析（PCA）

Principal Component Analysis, PCA

通俗易懂的描述：将数据投影到方差最大（方差越大，信息量越多）的几个相互正交（线性无关）的方向上。

K近邻

集成学习

Adaboost

随机森林（理论基础）

Sklearn

『行远见大』 Python 进阶篇：Sklearn 库