(持续更新中...)Leetcode 周赛记录
- 慢慢刷题慢慢补充~
- 写在最前面的小笔记(持续补充):
(1)ASCII码表:ASCII码中文站
(2)字符串数组用strings.sort()排序,sorted不适用
(3)Python字符串string类型不支持更改
(4)初始化一个字典用collections.defaultdict
(5)有序列表可以用sortedcontainers.SortedList
2022-08-14 第 306 场周赛
T1 6148. 矩阵中的局部最大值
模拟最大池化,Deep Learning 人狂喜
1 | |
T2 6149. 边积分最高的节点
1 | |
T3 6150. 根据模式串构造最小数字
我以为只有 T4 是原题,没想到 T3 居然也是原题 484. 寻找排列,而且还欺负我是穷逼不是会员看不到原题。

T4 6151. 统计特殊整数
看了赛后讨论区才发现是原题 1012. 至少有 1 位重复的数字,没意思。我还纳闷大家 Hard 题 A 得这么快。
2022-08-07 第 305 场周赛
动态规划专场了属于是,刚好我 DP 比较菜
T1 6136. 算术三元组的数目
给你一个下标从 0 开始、严格递增 的整数数组 nums 和一个正整数 diff 。如果满足下述全部条件,则三元组 (i, j, k) 就是一个 算术三元组 :
i < j < k,nums[j] - nums[i] == diff且nums[k] - nums[j] == diff
返回不同 算术三元组 的数目。
输入:nums = [0,1,4,6,7,10], diff = 3
输出:2
解释:
(1, 2, 4) 是算术三元组:7 - 4 == 3 且 4 - 1 == 3 。
(2, 4, 5) 是算术三元组:10 - 7 == 3 且 7 - 4 == 3 。
提示:
$3 \leq$ nums.length $\leq 200$
$0 \leq$ nums[i] $\leq 200$
$1 \leq$ diff $\leq 50$nums 严格 递增
1 | |
T2 6139. 受限条件下可到达节点的数目
现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 ,共有 n - 1 条边。
给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下,返回你可以从节点 0 到达的 最多 节点数目。
注意,节点 0 不 会标记为受限节点。
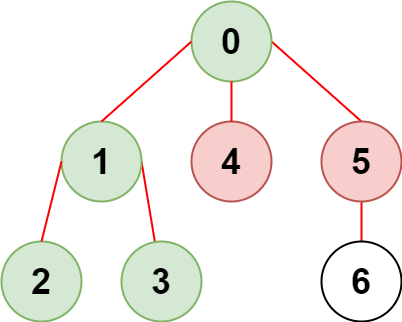
输入:n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出:4
解释:上图所示正是这棵树。
在不访问受限节点的前提下,只有节点 [0,1,2,3] 可以从节点 0 到达。
提示:
$2 \leq$ n $\leq 10^{5}$edges.length $== n - 1$edges[i].length $== 2$
$0 \leq a_{i}, b_{i} < n$
$a_{i} != b_{i}$edges 表示一棵有效的树
$1 \leq$ restricted.length $< n$
$1 \leq$ restricted[i] $< n$restricted 中的所有值 互不相同
从节点
0开始BFS即可。
1 | |
T3 6137. 检查数组是否存在有效划分
给你一个下标从 0 开始的整数数组 nums ,你必须将数组划分为一个或多个 连续 子数组。
如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种 有效 划分:
- 子数组 恰 由
2个相等元素组成,例如,子数组[2,2]。 - 子数组 恰 由
3个相等元素组成,例如,子数组[4,4,4]。 - 子数组 恰 由
3个连续递增元素组成,并且相邻元素之间的差值为1。例如,子数组[3,4,5],但是子数组[1,3,5]不符合要求。
如果数组 至少 存在一种有效划分,返回 true ,否则,返回 false 。
输入:nums = [4,4,4,5,6]
输出:true
解释:数组可以划分成子数组 [4,4] 和 [4,5,6] 。
这是一种有效划分,所以返回 true 。
提示:
$2 \leq$ nums.length $\leq 10^{5}$
$1 \leq$ nums[i] $\leq 10^{6}$
数据量小的情况下可以用递归,但本题用递归会
T……
1 | |
动态规划:遍历数组中的所有元素,判断该元素及其前的所有元素是否合法,更新当前的状态即可,当全部元素遍历完后即为最后结果。
(1)dp数组全部初始化为False:dp[0] = True, dp[1] = False;
若nums[0] == nums[1](条件一), 则dp[2] = True,否则为False;
若nums[0] == nums[1] == nums[2](条件二)或nums[0]+1 == nums[1] == nums[2]-1(条件三), 则dp[3] = True,否则为False;
(2)对于nums[i],有以下三种方式处理,状态转移规则为:
a. 若nums[i]与nums[i-1]按条件一组成子数组,则dp[i] = dp[i-2] & nums[i-1] == nums[i];
b. 若nums[i]与nums[i-1],nums[i-2]按条件二组成子数组,则dp[i] = dp[i-3] & nums[i-2] == nums[i-1] == nums[i];
c. 若nums[i]与nums[i-1],nums[i-2]按条件三组成子数组,则dp[i] = dp[i-3] & nums[i-2]+1 == nums[i-1] == nums[i]-1。
1 | |
T4 6138. 最长理想子序列
给你一个由小写字母组成的字符串 s ,和一个整数 k 。如果满足下述条件,则可以将字符串 t 视作是 理想字符串 :
t 是字符串 s 的一个子序列。t 中每两个 相邻 字母在字母表中位次的绝对差值小于或等于 k 。
返回 最长 理想字符串的长度。
字符串的子序列同样是一个字符串,并且子序列还满足:可以经由其他字符串删除某些字符(也可以不删除)但不改变剩余字符的顺序得到。
注意:字母表顺序不会循环。例如,'a' 和 'z' 在字母表中位次的绝对差值是 25 ,而不是 1 。
输入:s = “acfgbd”, k = 2
输出:4
解释:最长理想字符串是 “acbd” 。该字符串长度为 4 ,所以返回 4 。
注意 “acfgbd” 不是理想字符串,因为 ‘c’ 和 ‘f’ 的字母表位次差值为 3 。
提示:
$1 \leq$ s.length $\leq 10^{5}$
$0 \leq$ k $\leq 25$s 由小写英文字母组成
动态规划:
dp数组记录以某一字母结尾的最长理想字符串长度;对于s[i],其在字母表中的索引为t,以其结尾的最大长度,仅需考虑其[t-k, t+k]范围内的字母即可,而无需考虑s[i]之前的所有字母。
1 | |
2022-07-31 第 304 场周赛
T1 6132. 使数组中所有元素都等于零
给你一个非负整数数组 nums 。在一步操作中,你必须:
选出一个正整数 x ,x 需要小于或等于 nums 中 最小 的 非零 元素。nums 中的每个正整数都减去 x。
返回使 nums 中所有元素都等于 0 需要的 最少 操作数。
输入:nums = [1,5,0,3,5]
输出:3
解释:
第一步操作:选出 x = 1 ,之后 nums = [0,4,0,2,4] 。
第二步操作:选出 x = 2 ,之后 nums = [0,2,0,0,2] 。
第三步操作:选出 x = 2 ,之后 nums = [0,0,0,0,0] 。
提示:
$1 \leq$ nums.length $\leq 100$
$0 \leq$ nums[i] $\leq 100$
解题思路:
模拟:每次减掉数组中的最小非零元素即可,直到全部置零
1 | |
T2 6133. 分组的最大数量
给你一个正整数数组 grades ,表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组,其中分组间的顺序满足以下全部条件:
第 i 个分组中的学生总成绩 小于 第 (i + 1) 个分组中的学生总成绩,对所有组均成立(除了最后一组)。
第 i 个分组中的学生总数 小于 第 (i + 1) 个分组中的学生总数,对所有组均成立(除了最后一组)。
返回可以形成的 最大 组数。
输入:grades = [10,6,12,7,3,5]
输出:3
解释:下面是形成 3 个分组的一种可行方法:
-> 第 1 个分组的学生成绩为 grades = [12] ,总成绩:12 ,学生数:1
-> 第 2 个分组的学生成绩为 grades = [6,7] ,总成绩:6 + 7 = 13 ,学生数:2
-> 第 3 个分组的学生成绩为 grades = [10,3,5] ,总成绩:10 + 3 + 5 = 18 ,学生数:3
可以证明无法形成超过 3 个分组。
提示:
$1 \leq$ grades.length $\leq 10^{5}$
$1 \leq$ grades[i] $\leq 10^{5}$
又是脑筋急转弯,大无语
解题思路:
分组的形式可以是:将n个学生分成k组,每组人数为1、2、...、k,若 $\frac{k \times (k+1)}{2} < n$,即多出来m(< k+1)个学生,则将多出来的学生随机分配到前面的组内。按成绩有序分组则可以满足总成绩递增的原则。
1 | |
T3 6134. 找到离给定两个节点最近的节点
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
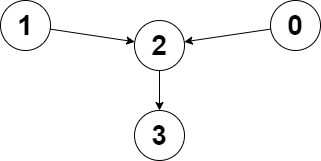
输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
提示:n == edges.length
$2 \leq$ n $\leq 10^{5}$
$-1 \leq$ edges[i] $<$ nedges[i] != i
$0 \leq$ node1, node2 $<$ n
解题思路:
从两个节点开始BFS,记录到每个节点的距离,最后选择二者均能到达且距离最小的即可。
1 | |
T4 6135. 图中的最长环
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
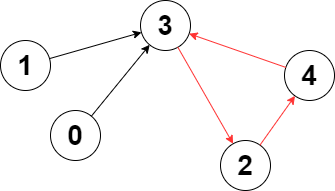
输入:edges = [3,3,4,2,3]
输出:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
提示:n == edges.length
$2 \leq$ n $\leq 10^{5}$
$-1 \leq$ edges[i] $<$ nedges[i] != i
解题思路:
做完T3,一种容易想到的思路是:从每个节点开始遍历整个有向图,若能到达自身节点则说明其处于环内,且距离为环的长度,遍历所有节点,更新最长环的长度即为答案。时间复杂度为 $O(N^{2}+N)$,超时无疑。
优化思路:
通过拓扑排序依次去除入度为0的节点后,仅保留处于闭环内的节点,再通过上述方式遍历,且每个节点仅需访问一遍, 可将visit数组置于循环外。时间复杂度为 $O(N)$ 。
1 | |
2022-07-24 第 303 场周赛
T1 6124. 第一个出现两次的字母
给你一个由小写英文字母组成的字符串 s ,请你找出并返回第一个出现 两次 的字母。
注意:
- 如果 a 的 第二次 出现比 b 的 第二次 出现在字符串中的位置更靠前,则认为字母 a 在字母 b 之前出现两次。
- s 包含至少一个出现两次的字母。
输入:s = “abccbaacz”
输出:”c”
解释:
字母 ‘a’ 在下标 0 、5 和 6 处出现。
字母 ‘b’ 在下标 1 和 4 处出现。
字母 ‘c’ 在下标 2 、3 和 7 处出现。
字母 ‘z’ 在下标 8 处出现。
字母 ‘c’ 是第一个出现两次的字母,因为在所有字母中,’c’ 第二次出现的下标是最小的。
提示:
$2 \leq$ s.length $\leq 100$s 由小写英文字母组成s 包含至少一个重复字母
解题思路:
哈希表+模拟
1 | |
T2 6125. 相等行列对
给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ,返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。
如果行和列以相同的顺序包含相同的元素(即相等的数组),则认为二者是相等的。
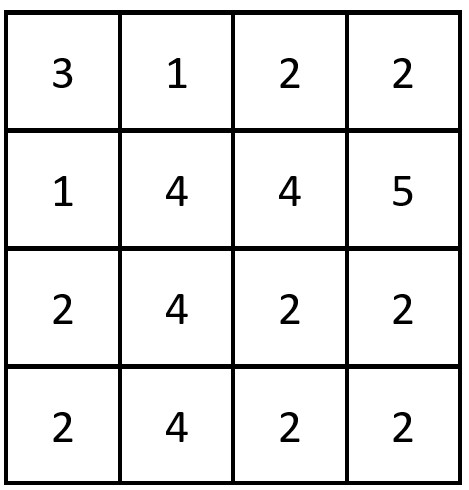
输入:grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出:3
解释:存在三对相等行列对:
-> (第 0 行,第 0 列):[3,1,2,2]
-> (第 2 行, 第 2 列):[2,4,2,2]
-> (第 3 行, 第 2 列):[2,4,2,2]
提示:n == grid.length == grid[i].length
$1 \leq$ n $\leq 200$
$1 \leq$ grid[i][j] $\leq 10^{5}$
解题思路:
暴力即可,对比每一行和每一列
1 | |
T3 6126. 设计食物评分系统
设计一个支持下述操作的食物评分系统:
修改 系统中列出的某种食物的评分。
返回系统中某一类烹饪方式下评分最高的食物。
实现 FoodRatings 类:
FoodRatings(String[] foods, String[] cuisines, int[] ratings)初始化系统。食物由foods、cuisines和ratings描述,长度均为n。foods[i]是第i种食物的名字。cuisines[i]是第i种食物的烹饪方式。ratings[i]是第i种食物的最初评分。void changeRating(String food, int newRating)修改名字为food的食物的评分。String highestRated(String cuisine)返回指定烹饪方式cuisine下评分最高的食物的名字。如果存在并列,返回 字典序较小 的名字。
注意:字符串x的字典序比字符串y更小的前提是:x在字典中出现的位置在y之前,也就是说,要么x是y的前缀,或者在满足x[i] != y[i]的第一个位置i处,x[i]在字母表中出现的位置在y[i]之前。
输入:
[“FoodRatings”, “highestRated”, “highestRated”, “changeRating”, “highestRated”, “changeRating”, “highestRated”]
[[[“kimchi”, “miso”, “sushi”, “moussaka”, “ramen”, “bulgogi”], [“korean”, “japanese”, “japanese”, “greek”, “japanese”, “korean”], [9, 12, 8, 15, 14, 7]], [“korean”], [“japanese”], [“sushi”, 16], [“japanese”], [“ramen”, 16], [“japanese”]]
输出:
[null, “kimchi”, “ramen”, null, “sushi”, null, “ramen”]
解释:
FoodRatings foodRatings = new FoodRatings([“kimchi”, “miso”, “sushi”, “moussaka”, “ramen”, “bulgogi”], [“korean”, “japanese”, “japanese”, “greek”, “japanese”, “korean”], [9, 12, 8, 15, 14, 7]);
foodRatings.highestRated(“korean”); // 返回 “kimchi”,kimchi” 是分数最高的韩式料理,评分为 9 。
foodRatings.highestRated(“japanese”); // 返回 “ramen”,”ramen” 是分数最高的日式料理,评分为 14 。
foodRatings.changeRating(“sushi”, 16); // “sushi” 现在评分变更为 16 。
foodRatings.highestRated(“japanese”); // 返回 “sushi”,”sushi” 是分数最高的日式料理,评分为 16 。
foodRatings.changeRating(“ramen”, 16); // “ramen” 现在评分变更为 16 。
foodRatings.highestRated(“japanese”); // 返回 “ramen”,”sushi” 和 “ramen” 的评分都是 16,但是,”ramen” 的字典序比 “sushi” 更小。
提示:
$1 \leq$ n $\leq 2 * 10^{4}$n == foods.length == cuisines.length == ratings.length
$1 \leq$ foods[i].length, cuisines[i].length $\leq 10$foods[i]、cuisines[i] 由小写英文字母组成
$1 \leq$ ratings[i] $\leq 10^{8}$foods 中的所有字符串 互不相同
在对 changeRating 的所有调用中,food 是系统中食物的名字。
在对 highestRated 的所有调用中,cuisine 是系统中 至少一种 食物的烹饪方式。
最多调用 changeRating 和 highestRated 总计 $2 * 10^{4}$ 次
解题思路:
建立映射: 将food[i]的烹饪方式cuisines[i]和 最初评分ratings[i]存入一个字典中。将cuisines[i]的下所有食物和最初评分存入一个字典中,并按照评分排序。
实现方式:
利用defaultdict建立字典,相比于dict,其可以避免字典中key值不存在时的KeyError异常,SortedList用于评分排序,其插入元素的时间复杂度为 $O(logn)$Dict + SortedList可以解决所有这类问题
defaultdict使用详解:defaultdict在初始化时可以提供一个default_factory的参数,default_factory接收一个工厂函数作为参数, 可以是int、str、list等内置函数,也可以是 自定义函数。其他方法与dict一致。
1 | |
T4 6127. 优质数对的数目
给你一个下标从 0 开始的正整数数组 nums 和一个正整数 k 。
如果满足下述条件,则数对 (num1, num2) 是 优质数对 :
num1和num2都 在数组nums中存在。num1 OR num2和num1 AND num2的二进制表示中值为1的位数之和大于等于k,其中OR是按位 或 操作,而AND是按位 与 操作。
返回 不同 优质数对的数目。
如果 a != c 或者 b != d ,则认为 (a, b) 和 (c, d) 是不同的两个数对。例如,(1, 2) 和 (2, 1) 不同。
注意:如果 num1 在数组中至少出现 一次 ,则满足 num1 == num2 的数对 (num1, num2) 也可以是优质数对。
输入:nums = [1,2,3,1], k = 3
输出:5
解释:有如下几个优质数对:
-> (3, 3):(3 AND 3) 和 (3 OR 3) 的二进制表示都等于 (11) 。值为 1 的位数和等于 2 + 2 = 4 ,大于等于 k = 3 。
-> (2, 3) 和 (3, 2): (2 AND 3) 的二进制表示等于 (10) ,(2 OR 3) 的二进制表示等于 (11) 。值为 1 的位数和等于 1 + 2 = 3 。
-> (1, 3) 和 (3, 1): (1 AND 3) 的二进制表示等于 (01) ,(1 OR 3) 的二进制表示等于 (11) 。值为 1 的位数和等于 1 + 2 = 3 。
所以优质数对的数目是 5 。
提示:
$1 \leq$ nums.length $\leq 10^{5}$
$1 \leq$ nums[i] $\leq 10^{9}$
$1 \leq$ k $\leq 60$
1 | |
2022-07-23 第 83 场双周赛
T1 6128. 最好的扑克手牌
给你一个整数数组 ranks 和一个字符数组 suit 。你有 5 张扑克牌,第 i 张牌大小为 ranks[i] ,花色为 suits[i] 。
下述是从好到坏你可能持有的 手牌类型 :
1、"Flush":同花,五张相同花色的扑克牌。
2、"Three of a Kind":三条,有 3 张大小相同的扑克牌。
3、"Pair":对子,两张大小一样的扑克牌。
4、"High Card":高牌,五张大小互不相同的扑克牌。
请你返回一个字符串,表示给定的 5 张牌中,你能组成的 最好手牌类型 。
注意:返回的字符串 大小写 需与题目描述相同。
输入:ranks = [4,4,2,4,4], suits = [“d”,”a”,”a”,”b”,”c”]
输出:”Three of a Kind”
解释:第一、二和四张牌组成三张相同大小的扑克牌,所以得到 “Three of a Kind” 。
注意我们也可以得到 “Pair” ,但是 “Three of a Kind” 是更好的手牌类型。
有其他的 3 张牌也可以组成 “Three of a Kind” 手牌类型。
提示:ranks.length == suits.length == 5
1 $\leq$ ranks[i] $\leq$ 13
‘a’ $\leq$ suits[i] $\leq$ ‘d’
任意两张扑克牌不会同时有相同的大小和花色。
解题思路:
直接模拟即可
1 | |
T2 6129. 全 0 子数组的数目
给你一个整数数组 nums ,返回全部为 0 的 子数组 数目。
子数组 是一个数组中一段连续非空元素组成的序列。
输入:nums = [0,0,0,2,0,0]
输出:9
解释:
子数组 [0] 出现了 5 次。
子数组 [0,0] 出现了 3 次。
子数组 [0,0,0] 出现了 1 次。
不存在长度大于 3 的全 0 子数组,所以我们返回 9 。
提示:
$1 \leq$ nums.length $\leq 10^{5}$
$-10^{9} \leq$ nums[i] $\leq 10^{9}$
解题思路:
数学题:记录连续的0的个数,然后对于每个连续长度为n的0序列,其中包含了长度n-k+1个为k的0序列,(如一个长度为3的0序列,其包含了3个长度为1,2个长度为2,1个长度为3的0序列)。易知,长度为n的0序列包含了 $\sum_{i=1}^{n}i$ 个全0子数组。对每个0序列的长度计算以上值累加即为答案。
1 | |
T3 6130. 设计数字容器系统
设计一个数字容器系统,可以实现以下功能:
在系统中给定下标处 插入 或者 替换 一个数字。
返回 系统中给定数字的最小下标。
请你实现一个 NumberContainers 类:
NumberContainers() 初始化数字容器系统。void change(int index, int number) 在下标 index 处填入 number 。如果该下标 index 处已经有数字了,那么用 number 替换该数字。int find(int number) 返回给定数字 number 在系统中的最小下标。如果系统中没有 number ,那么返回 -1 。
输入:
[“NumberContainers”, “find”, “change”, “change”, “change”, “change”, “find”, “change”, “find”]
[[], [10], [2, 10], [1, 10], [3, 10], [5, 10], [10], [1, 20], [10]]
输出:
[null, -1, null, null, null, null, 1, null, 2]
解释:
NumberContainers nc = new NumberContainers();
nc.find(10); // 没有数字 10 ,所以返回 -1 。
nc.change(2, 10); // 容器中下标为 2 处填入数字 10 。
nc.change(1, 10); // 容器中下标为 1 处填入数字 10 。
nc.change(3, 10); // 容器中下标为 3 处填入数字 10 。
nc.change(5, 10); // 容器中下标为 5 处填入数字 10 。
nc.find(10); // 数字 10 所在的下标为 1 ,2 ,3 和 5 。因为最小下标为 1 ,所以返回 1 。
nc.change(1, 20); // 容器中下标为 1 处填入数字 20 。注意,下标 1 处之前为 10 ,现在被替换为 20 。
nc.find(10); // 数字 10 所在下标为 2 ,3 和 5 。最小下标为 2 ,所以返回 2 。
提示:
$1 \leq$ index, number $\leq 10^{9}$
调用 change 和 find 的 总次数 不超过 $10^{5}$ 次。
Python数据结构还是掌握得不够,Sortedlist居然不会用。除以下特殊方法外,其他方法与列表基本一致。
1 | |
1 | |
T4 6131. 不可能得到的最短骰子序列
给你一个长度为 n 的整数数组 rolls 和一个整数 k 。你扔一个 k 面的骰子 n 次,骰子的每个面分别是 1 到 k ,其中第 i 次扔得到的数字是 rolls[i] 。
请你返回 无法 从 rolls 中得到的 最短 骰子子序列的长度。
扔一个 k 面的骰子 len 次得到的是一个长度为 len 的 骰子子序列 。
注意 ,子序列只需要保持在原数组中的顺序,不需要连续。
输入:rolls = [4,2,1,2,3,3,2,4,1], k = 4
输出:3
解释:所有长度为 1 的骰子子序列 [1] ,[2] ,[3] ,[4] 都可以从原数组中得到。
所有长度为 2 的骰子子序列 [1, 1] ,[1, 2] ,… ,[4, 4] 都可以从原数组中得到。
子序列 [1, 4, 2] 无法从原数组中得到,所以我们返回 3 。
还有别的子序列也无法从原数组中得到。
提示:n == rolls.length
$1 \leq$ n $\leq 10^{5}$
$1 \leq$ rolls[i] $\leq$ k $\leq 10^{5}$
1 | |
2022-07-17 第 302 场周赛
T1 6120. 数组能形成多少数对
给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤:
从 nums 选出 两个 相等的 整数
从 nums 中移除这两个整数,形成一个 数对
请你在 nums 上多次执行此操作直到无法继续执行。
返回一个下标从 0 开始、长度为 2 的整数数组 answer 作为答案,其中 answer[0] 是形成的数对数目,answer[1] 是对 nums 尽可能执行上述操作后剩下的整数数目。
输入:nums = [1,3,2,1,3,2,2]
输出:[3,1]
解释:
nums[0] 和 nums[3] 形成一个数对,并从 nums 中移除,nums = [3,2,3,2,2] 。
nums[0] 和 nums[2] 形成一个数对,并从 nums 中移除,nums = [2,2,2] 。
nums[0] 和 nums[1] 形成一个数对,并从 nums 中移除,nums = [2] 。
无法形成更多数对。总共形成 3 个数对,nums 中剩下 1 个数字。
提示:
$1 \leq nums.length \leq 100$
$1 \leq nums[i] \leq 100$
愉快的签到题~一上来肾上腺素飙升,WA了两发(🙂🙂🙂
1 | |
T2 6164. 数位和相等数对的最大和
给你一个下标从 0 开始的数组 nums ,数组中的元素都是 正 整数。请你选出两个下标 i 和 j(i != j),且 nums[i] 的数位和与 nums[j] 的数位和相等。
请你找出所有满足条件的下标 i 和 j ,找出并返回 nums[i] + nums[j] 可以得到的 最大值 。
输入:nums = [18,43,36,13,7]
输出:54
解释:满足条件的数对 (i, j) 为:
-> (0, 2) ,两个数字的数位和都是 9 ,相加得到 18 + 36 = 54 。
-> (1, 4) ,两个数字的数位和都是 7 ,相加得到 43 + 7 = 50 。
所以可以获得的最大和是 54 。
提示:
$1 \leq nums.length \leq 10^{5}$
$1 \leq nums[i] \leq 10^{9}$
看了眼数据量,最大和值为
9×9=81,直接哈希表记录,haspmap[i]为数位和为i的整数列表,返回列表长度大于2且列表中最大的两个元素之和,遍历hashmap更新结果
1 | |
T3 6121. 裁剪数字后查询第 K 小的数字
给你一个下标从 0 开始的字符串数组 nums ,其中每个字符串 长度相等 且只包含数字。
再给你一个下标从 0 开始的二维整数数组 queries ,其中 queries[i] = [ki, trimi] 。对于每个 queries[i] ,你需要:
将 nums 中每个数字 裁剪 到剩下 最右边 trimi 个数位。
在裁剪过后的数字中,找到 nums 中第 ki 小数字对应的 下标 。如果两个裁剪后数字一样大,那么下标 更小 的数字视为更小的数字。
将 nums 中每个数字恢复到原本字符串。
请你返回一个长度与 queries 相等的数组 answer,其中 answer[i] 是第 i 次查询的结果。
输入:nums = [“102”,”473”,”251”,”814”], queries = [[1,1],[2,3],[4,2],[1,2]]
输出:[2,2,1,0]
解释:
查询 1. 裁剪到只剩 1 个数位后,nums = [“2”,”3”,”1”,”4”] 。最小的数字是 1 ,下标为 2 。
查询 2. 裁剪到剩 3 个数位后,nums 没有变化。第 2 小的数字是 251 ,下标为 2 。
查询 3. 裁剪到剩 2 个数位后,nums = [“02”,”73”,”51”,”14”] 。第 4 小的数字是 73 ,下标为 1 。
查询 4. 裁剪到剩 2 个数位后,最小数字是 2 ,下标为 0 。
注意,裁剪后数字 “02” 值为 2 。
提示:
裁剪到剩下 x 个数位的意思是不断删除最左边的数位,直到剩下 x 个数位。nums 中的字符串可能会有前导 0 。
$1 \leq nums.length \leq 100$
$1 \leq nums[i].length \leq 100$nums[i] 只包含数字。
所有 nums[i].length 的长度 相同 。
$1 \leq queries.length \leq 100$
$queries[i].length == 2$
$1 \leq k_{i} \leq nums.length$
$1 \leq trim_{i} \leq nums[0].length$
这题和第四题换一下位置还行,这点数据量,写半天超时,找不到哪里出了死循环……儒哥更惨 👇👇👇
TLE的代码 👇👇👇
1 | |
赛后,看了眼大家的写法,才意识到字符串可以直接排序,不一定非要转换成整数,字符串转化成整数的过程嵌套在双层循环中,时间复杂度爆炸。
以下为AC的代码 👇👇👇
1 | |
T4 6122. 使数组可以被整除的最少删除次数
给你两个正整数数组 nums 和 numsDivide 。你可以从 nums 中删除任意数目的元素。
请你返回使 nums 中 最小 元素可以整除 numsDivide 中所有元素的 最少 删除次数。如果无法得到这样的元素,返回 -1 。
如果 y % x == 0 ,那么我们说整数 x 整除 y 。
输入:nums = [2,3,2,4,3], numsDivide = [9,6,9,3,15]
输出:2
解释:
[2,3,2,4,3] 中最小元素是 2 ,它无法整除 numsDivide 中所有元素。
我们从 nums 中删除 2 个大小为 2 的元素,得到 nums = [3,4,3] 。
[3,4,3] 中最小元素为 3 ,它可以整除 numsDivide 中所有元素。
可以证明 2 是最少删除次数。
提示:
$1 \leq nums.length, numsDivide.length \leq 10^{5}$
$1 \leq nums[i], numsDivide[i] \leq 10^{9}$
Hard……
问题等价于求在有序的nums中,能够被numsDivide中所有元素的最大公约数整除的最小元素的位置索引
1 | |
2022-07-13 蔚来 2023 届提前批笔试
T2 最少的操作次数
小红可以对一个数进行如下两种操作:将这个数乘以 $x$,或将这个数乘以 $y$。操作次数是没有限制的。小红想知道,自己最少经过多少次操作以后,可以把 $a$ 变成 $b$ ?
输入描述:
四个正整数 $x, y, a, b$,用空格隔开。
$2 \leq x, y \leq 100$
$1 \leq a, b \leq 10^{9}$
输出描述:
如果小红无论如何都无法把 $a$ 变成 $b$,则输出 $-1$。否则输出小红操作的最少次数,可以证明,如果存在某种操作,那么最少次数一定是固定的。
示例输入:
2 3 5 20
示例输出:
2
解释:
x = 2,y = 3,进行两次乘 2 操作,可以把 5 变成 20。
1 | |
T3 牛牛的开心旅行
牛牛对 $n$ 个城市的旅游情况进行了规划。
已知每个城市有两种属性 $x_{i}$ 和 $y_{i}$,其中 $x_{i}$ 表示去第 $i$ 号城市的花费,$y_{i}$ 表示在第 $i$ 号城市游玩后会得到的开心值。
现在牛牛希望从中挑选一些城市去游玩,但挑选出的城市必须满足任意两个城市之间花费的绝对值小于 $k$。
他想请你帮他计算出在满足上述条件下能得到的最大开心值是多少。
输入描述:
第一行输入两个正整数 $n$和 $k$。
接下来 $n$ 行,每行输入两个正整数 $x_{i}$ 和 $y_{i}$,分别表示每个城市的两种属性。
$1 \leq n \leq 10^{5}$
$1 \leq k \leq 10^{9}$
$1 \leq x_{i}, y_{i} \leq 10^{9}$
输出描述:
输出一个整数表示答案。
示例输入:
5 3
1 3
2 1
5 2
3 1
4 3
示例输出:
6
解释:
牛牛可以选择去 3 号, 4 号和 5 号城市进行游玩,并收获最大的开心值。
1 | |
2022-07-10 第 301 场周赛
前一天晚上的双周赛太太太难了,给我整自闭了,问了一下儒哥,也觉得最近周赛难度上升了,跟公司笔试难度不匹配…..
然后上午的周赛A了三道,虽然有点慢,但我不自闭了
T1. 6112. 装满杯子需要的最短总时长
现有一台饮水机,可以制备冷水、温水和热水。每秒钟,可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。
给你一个下标从 0 开始、长度为 3 的整数数组 amount ,其中 amount[0]、amount[1] 和 amount[2] 分别表示需要装满冷水、温水和热水的杯子数量。返回装满所有杯子所需的 最少 秒数。
输入:amount = [1,4,2]
输出:4
解释:下面给出一种方案:
第 1 秒:装满一杯冷水和一杯温水。
第 2 秒:装满一杯温水和一杯热水。
第 3 秒:装满一杯温水和一杯热水。
第 4 秒:装满一杯温水。
可以证明最少需要 4 秒才能装满所有杯子。
解题思路:
简易贪心 — 每次装水都选择剩余最多的两种类型的杯子。
1 | |
T2. 6113. 无限集中的最小数字
现有一个包含所有正整数的集合 [1, 2, 3, 4, 5, ...]。
实现 SmallestInfiniteSet 类:
SmallestInfiniteSet()初始化SmallestInfiniteSet对象以包含所有正整数。int popSmallest()移除 并返回该无限集中的最小整数。void addBack(int num)如果正整数num不 存在于无限集中,则将一个num添加 到该无限集中。
输入
[“SmallestInfiniteSet”, “addBack”, “popSmallest”, “popSmallest”, “popSmallest”, “addBack”, “popSmallest”, “popSmallest”, “popSmallest”]
[[], [2], [], [], [], [1], [], [], []]
输出
[null, null, 1, 2, 3, null, 1, 4, 5]
解释
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 已经在集合中,所以不做任何变更。
smallestInfiniteSet.popSmallest(); // 返回 1 ,因为 1 是最小的整数,并将其从集合中移除。
smallestInfiniteSet.popSmallest(); // 返回 2 ,并将其从集合中移除。
smallestInfiniteSet.popSmallest(); // 返回 3 ,并将其从集合中移除。
smallestInfiniteSet.addBack(1); // 将 1 添加到该集合中。
smallestInfiniteSet.popSmallest(); // 返回 1 ,因为 1 在上一步中被添加到集合中,且 1 是最小的整数,并将其从集合中移除。
smallestInfiniteSet.popSmallest(); // 返回 4 ,并将其从集合中移除。
smallestInfiniteSet.popSmallest(); // 返回 5 ,并将其从集合中移除。
解题思路:
别问,问就是哈希表 — 建立一个pop_list记录已被移除的元素。
(1)popSmallest()操作:检验pop_list中元素pop_list[i]与其下标i是否满足pop_list[i] == i+1,不满足则说明i+1还在无限集合中,返回i+1即可,否则返回最后一个元素的下一个数字pop_list[-1]+1,并将返回结果添加至pop_list中。
(2)addBack(num)操作:直接从pop_list中移除num即可。
时间复杂度: $O(M \times NlogN)$,$M$ 为调用各方法的次数,空间复杂度: $O(N)$
1 | |
T3. 6114. 移动片段得到字符串
给你两个字符串 start 和 target ,长度均为 n 。每个字符串 仅 由字符 'L'、'R' 和 '_' 组成,其中:
- 字符
'L'和'R'表示片段,其中片段'L'只有在其左侧直接存在一个空位时才能向左移动,而片段'R'只有在其右侧直接存在一个空位时才能向右移动。 - 字符
'_'表示可以被 任意'L'或'R'片段占据的空位。
如果在移动字符串 start 中的片段任意次之后可以得到字符串 target ,返回 true ;否则,返回 false 。
输入:start = “_L__R__R_”, target = “L______RR”
输出:true
解释:可以从字符串 start 获得 target ,需要进行下面的移动:
-> 将第一个片段向左移动一步,字符串现在变为 “L___R__R_” 。
-> 将最后一个片段向右移动一步,字符串现在变为 “L___R___R” 。
-> 将第二个片段向右移动散步,字符串现在变为 “L______RR” 。
可以从字符串 start 得到 target ,所以返回 true 。
解题思路:
还是哈希表 — 分别记录start和target中'L'和'R'出现的顺序和位置索引,若顺序不一致则直接返回false,否则进一步判断start中每一个'L'和'R'的位置的合法性。
遍历所有'L'的索引,对于第i个'L', 其在start中的位置索引不能小于在target中的索引,即左侧。
遍历所有'R'的索引,对于第i个'R', 其在start中的位置索引不能大于在target中的索引,即右侧。
时间复杂度: $O(N)$,空间复杂度: $O(N)$
1 | |
T4. 6115. 统计理想数组的数目
给你两个整数 n 和 maxValue ,用于描述一个 理想数组 。
对于下标从 0 开始、长度为 n 的整数数组 arr ,如果满足以下条件,则认为该数组是一个 理想数组 :
- 每个
arr[i]都是从1到maxValue范围内的一个值,其中0 <= i < n。 - 每个
arr[i]都可以被arr[i - 1]整除,其中0 < i < n。
返回长度为 n 的 不同 理想数组的数目。由于答案可能很大,返回对 10^9 + 7 取余的结果。
输入:n = 2, maxValue = 5
输出:10
解释:存在以下理想数组:
-> 以 1 开头的数组(5 个):[1,1]、[1,2]、[1,3]、[1,4]、[1,5]
-> 以 2 开头的数组(2 个):[2,2]、[2,4]
-> 以 3 开头的数组(1 个):[3,3]
-> 以 4 开头的数组(1 个):[4,4]
-> 以 5 开头的数组(1 个):[5,5]
共计 5 + 2 + 1 + 1 + 1 = 10 个不同理想数组。
解题思路:
1 | |
2022-07-09 第 82 场双周赛
晚上十点半开始的周赛,晚上十一点才想起来自己报名了,第一次参加周赛就给我来了个下马威……
T1. 6116. 计算布尔二叉树的值
给你一棵 完整二叉树 的根,这棵树有以下特征:叶子节点 要么值为 0 要么值为 1 ,其中 0 表示 False ,1 表示 True 。非叶子节点 要么值为 2 要么值为 3 ,其中 2 表示逻辑或 OR ,3 表示逻辑与 AND 。计算 一个节点的值方式如下:
如果节点是个叶子节点,那么节点的 值 为它本身,即 True 或者 False 。
否则,**计算** 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。叶子节点 是没有孩子的节点。
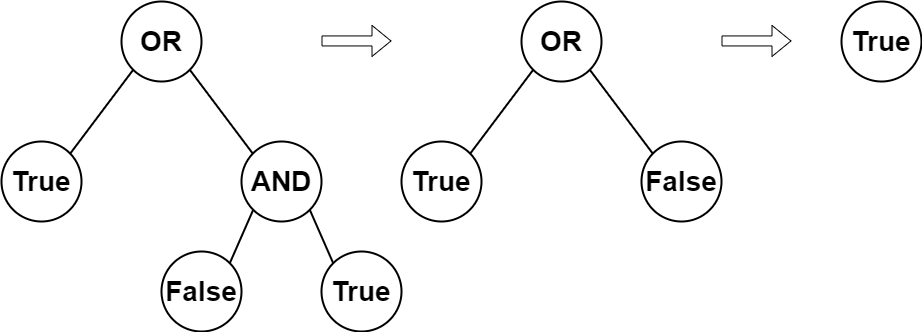
输入:root = [2,1,3,null,null,0,1]
输出:true
解释:上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ,所以我们返回 true 。
解题思路:
递归 — 由于是完整二叉树,只包含叶子节点和“伪根节点”,叶子节点直接返回,“伪根节点”返回运算结果。
时间复杂度: $O(N)$,空间复杂度: $O(1)$
1 | |
T2. 6117. 坐上公交的最晚时间
给你一个下标从 0 开始长度为 n 的整数数组 buses ,其中 buses[i] 表示第 i 辆公交车的出发时间。同时给你一个下标从 0 开始长度为 m 的整数数组 passengers ,其中 passengers[j] 表示第 j 位乘客的到达时间。所有公交车出发的时间互不相同,所有乘客到达的时间也互不相同。
给你一个整数 capacity ,表示每辆公交车 最多 能容纳的乘客数目。
每位乘客都会搭乘下一辆有座位的公交车。如果你在 y 时刻到达,公交在 x 时刻出发,满足 y <= x 且公交没有满,那么你可以搭乘这一辆公交。**最早** 到达的乘客优先上车。
返回你可以搭乘公交车的最晚到达公交站时间。你 不能 跟别的乘客同时刻到达。
注意:数组 buses 和 passengers 不一定是有序的。
输入:buses = [10,20], passengers = [2,17,18,19], capacity = 2
输出:16
解释:
第 1 辆公交车载着第 1 位乘客。
第 2 辆公交车载着你和第 2 位乘客。
注意你不能跟其他乘客同一时间到达,所以你必须在第二位乘客之前到达。
解题思路:
模拟:周赛的时候只想着模拟,满脑子都是模拟,最后感觉要过了,提交了四五次都有问题……自闭从此开始
1 | |
T3. 6118. 最小差值平方和
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度为 n 。
数组 nums1 和 nums2 的 差值平方和 定义为所有满足 0 <= i < n 的 (nums1[i] - nums2[i])^2 之和。
同时给你两个正整数 k1 和 k2 。你可以将 nums1 中的任意元素 +1 或者 -1 至多 k1 次。类似的,你可以将 nums2 中的任意元素 +1 或者 -1 至多 k2 次。
请你返回修改数组 nums1 至多 k1 次且修改数组 nums2 至多 k2 次后的最小 差值平方和 。
注意:你可以将数组中的元素变成 负 整数。
输入:nums1 = [1,4,10,12], nums2 = [5,8,6,9], k1 = 1, k2 = 1
输出:43
解释:一种得到最小差值平方和的方式为:
-> 将 nums1[0] 增加一次。
-> 将 nums2[2] 增加一次。
最小差值平方和为:
(2 - 5)^2 + (4 - 8)^2 + (10 - 7)^2 + (12 - 9)^2 = 43 。
注意,也有其他方式可以得到最小差值平方和,但没有得到比 43 更小答案的方案。
解题思路:
1 | |
T4. 6119. 元素值大于变化阈值的子数组
给你一个整数数组 nums 和一个整数 threshold 。
找到长度为 k 的 nums 子数组,满足数组中 每个 元素都 大于 threshold / k 。
请你返回满足要求的 任意 子数组的 大小 。如果没有这样的子数组,返回 -1 。子数组 是数组中一段连续非空的元素序列。
输入:nums = [6,5,6,5,8], threshold = 7
输出:1
解释:子数组 [8] 大小为 1 ,且 8 > 7 / 1 = 7 。所以返回 1 。
注意子数组 [6,5] 大小为 2 ,每个元素都大于 7 / 2 = 3.5 。
类似的,子数组 [6,5,6] ,[6,5,6,5] ,[6,5,6,5,8] 都是符合条件的子数组。
所以返回 2, 3, 4 和 5 都可以。
解题思路:
1 | |
以下为常用方法,方便速查使用
Python篇
常用数据结构及其操作
列表(List)
$\looparrowright$ 方法
1 | |
元组(Tuple)
$\looparrowright$ 操作大致与列表一致,区别在于元组的元素不能修改或删除,只能删除整个元组。
字典(Dictionary)
$\looparrowright$ 可变容器模型,可存储任意类型对象。
$\looparrowright$ 方法
1 | |
字符串
$\looparrowright$ 方法
1 | |
常用内置函数(按函数名首字母排序)
- all
$\looparrowright$ 判断给定对象中的所有元素是否都为True,如果是返回True,否则返回False(元素为0/NULL/False),使用示例:
1 | |
- any
$\looparrowright$ 判断给定对象中的所有元素是否都为False,如果是返回False,否则返回True,使用示例:
1 | |
- cmp
$\looparrowright$ 用于比较2个对象x,y,如果x < y,返回-1, 如果x == y返回0, 如果x > y返回1。
1 | |
- enumerate
$\looparrowright$ 将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在for循环当中,使用示例:
1 | |
- hash
$\looparrowright$ 获取对象(字符串或者数值等)的哈希值,使用示例:
1 | |
- map
$\looparrowright$ 根据提供的函数对指定序列做映射。
1 | |
- ord
$\looparrowright$ chr()函数(对于8位的ASCII字符串)或unichr()函数(对于Unicode对象)的配对函数,它以一个字符(长度为1的字符串)作为参数,返回对应的ASCII数值,或者Unicode数值,如果所给的Unicode字符超出了你的Python定义范围,则会引发一个TypeError的异常。
1 | |
- reverse
$\looparrowright$ 反向列表元素,使用示例:
1 | |
- set
$\looparrowright$ 创建输入对象的无序不重复元素集,set之间可以进行交集(&)、差集(-)、并集(|)运算,使用示例:
1 | |
- sorted
$\looparrowright$ 对给定对象进行排序。(sorted(iterable, cmp=None, key=None, reverse=False))
1 | |
- zip
$\looparrowright$ zip([a, b, c, …]),将可迭代对象a,b,c,…打包成元组,返回元组组成的列表,使用示例:
1 | |
C/C++篇
常用数据结构及其操作
向量(Vector)
$\looparrowright$ 动态大小数组的顺序容器,vector能够存放任意类型的动态数组。可以对序列中的任意元素进行快速直接访问,并利用指针进行操作。
$\Rightarrow$ 常用操作如下:
1 | |